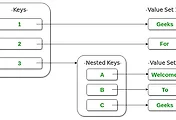
tree
tree 는 일반적으로 대상 정보들의 각 항목들을 계층적으로 연결하여 구조화 시키고자 할 때 사용하는 비선형 자료구조이다. graph 의 한 종류로, node 들의 집합으로 이루어져있다. 노드는 데이터를 가지고 있는 트리 구조의 교점을 의미한다. 각 노드들은 단순한 나열이 아닌 부모-자식 관계의 계층적 구조로 표현되어 있으며, 서로 다른 자식을 가진다.
binary tree
이진트리는 최대 차수가 2인 트리를 말한다. 하나의 노드에 left or right 방향으로 하나의 자식 노드만이 존재한다.
아래의 이미지처럼 한 쪽으로 편향된 이진트리의 유형을 편향 이진트리 라고 한다.

편향 이진 트리는 가장 끝의 leaf node 를 탐색할 경우 이전의 노드들을 전부 읽어야 한다는 단점이 있어서 다소 효율이 떨어지는 편이다.
leaf node 를 제외한 모든 노드의 차수가 두개로 이루어진 아래의 이미지와 같은 유형을 포화 이진트리라고 한다.

이 경우는 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있어, 파악이 용이하다는 장점이 있다.
포화이진트리는 완전 이진트리에 포함되기도 한다. 완전 이진트리란 노드가 왼쪽부터 생성되는 이진트리를 말한다.

위 이미지의 하단부에 있는 트리들은 1) 1번 노드에 왼쪽 오른쪽 두 개의 자식 노드가 존재하지 않고 2) 왼쪽에 위치한 2번 노드의 자식이 다 만들어진 후 3번 노드의 자식이 만들어져야 하는데 그렇지 않았으며 3) 2번 노드가 왼쪽부터 자식이 만들어지지 않았고 3) 2번과 마찬가지로 2번 노드의 자식이 만들어진 후 3번 노드의 자식이 만들어져야 하는데 그렇지 않았으므로 완전 이진트리가 될 수 없다.
이진트리의 탐색
아래 이미지는 [21, 28, 14, 32, 25, 18, 11, 30, 19, 15]의 순서로 주어지는 값으로부터 이진 탐색 트리를 구축하는 과정을 보여준다

여기에서 27을 찾기 위해서는 아래의 이미지대로 찾는다.
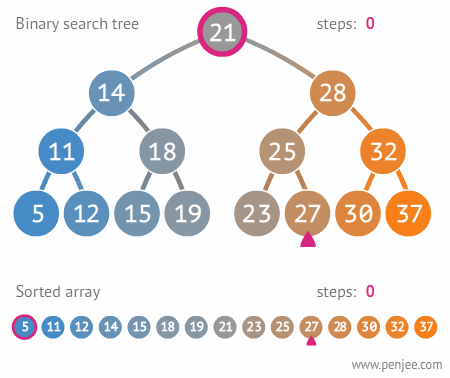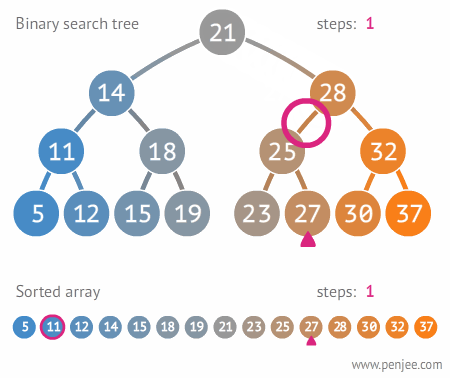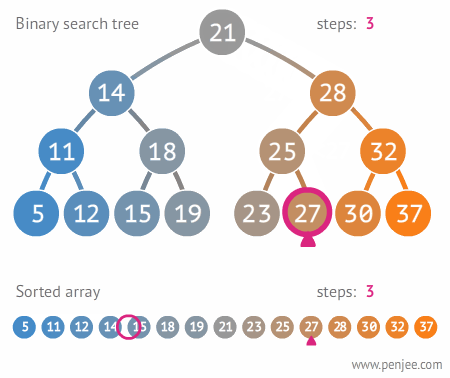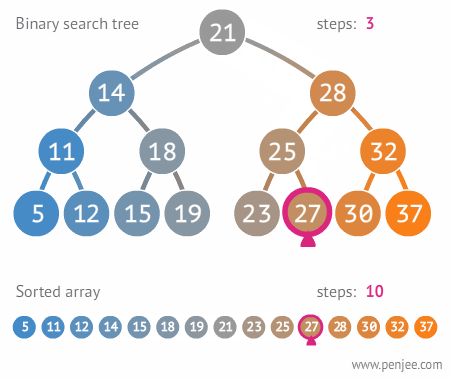
이진트리는 항상 부모 노드가 왼쪽 자식 노드보다는 크고 오른쪽 자식 노드보다 작으므로, 한번 탐색할 때 마다 보아야 하는 원소의 개수가 절반씩 줄어든다는 장점이 있다.
binary search tree code
이진트리를 탐색하는 코드를 구현하기 위해서는 먼저 class 를 정의하고, insert method 와 find method 를 만들어야 한다.
class NodeStudy():
def __init__(self, data):
self.data = data
self.left = self.right = None
class BinarySearchTree():
def __init__(self):
self.root = None
def insert(self, data):
self.root = self._insert_value(self.root, data)
return self.root is not None
def _insert_value(self, node, data):
if node is None:
node = Node(data)
else:
if data <= node.data:
node.left = self._insert_value(node.left, data)
else:
node.right = self._insert_value(node.right,data)
return node
def find(self, key):
return self._find_value(self.root, key)
def _find_value(self, root, key):
if root is None or root.data == key:
return root is not None
elif key < root.data:
return self._find_value(root.left, key)
else:
return self._find_value(root.right, key)이진트리 순회 알고리즘
데이터 탐색 속도 증진을 위해 사용하는 구조이다.
[40, 20, 50, 10, 30, 70, 60] 을 이진트리 기법으로 넣으면 아래의 이미지와 같다.

해당 tree 를 탐색해보자.
전위순회 pre-order traversal
깊이 우선 탐색DFS 중 하나로, root -> left child node -> right child node 순서로 탐색한다.
def pre_order(self):
def _pre_order_(root):
if root is None:
pass
else:
print(root.data)
_pre_order_(root.left)
_pre_order_(root.right)
_pre_order_(self.root)즉, [40, 20, 10, 30, 50, 70, 60] 이 출력된다.
중위순회 in-order traversal
left child node -> root -> right child node
이진 탐색 트리를 정순회하면 정렬된 데이터를 얻을 수 있다.
def in_order(self):
def _in_order_(root):
if root is None:
pass
else:
_in_order_(root.left)
print(root.data)
_in_order_(root.right)
_in_order_(self.root)[10, 20, 30, 40, 50, 60, 70] 이 출력된다.
후위순회 post-order traversal
left child node -> child node -> root
def post_order(self):
def _post_order_(root):
if root is None:
pass
else:
_post_order_(root.left)
_post_order_(root.right)
print(root.data)
_post_order_(self.root)[10, 30, 20, 60, 70, 50, 40] 이 출력된다.
레벨순회 lever-order traversal
레벨순회는 맨 위의 root node 부터 깊이 순으로 방문한다. [40, 20, 50, 10, 30, 70, 60] 순으로 출력될것이다.
'python' 카테고리의 다른 글
| dictionary & hash (0) | 2021.04.27 |
|---|---|
| stack & queue (0) | 2021.04.27 |
| array & tuple & set (0) | 2021.04.27 |
| args & kwargs (0) | 2021.04.27 |
| set (0) | 2021.04.27 |